Top 13 Common Mistakes to Avoid in PSLE Math

How many times have you heard your child's Math teacher saying that your child would have done much better if he/she had read examination questions more carefully and avoided some common mistakes?

It is frustrating for both parents and child when marks are lost in examinations unnecessarily.

Other than transfer errors (copying numbers wrongly from the question stem), this article shows a compilation of some common mistakes that are frequently made by students in upper primary levels.

• 1. Subtract...From...

  Common Mistake / Misconception

  Subtract 4y from 6
  Answer: 4y – 6 (wrong!)

  Correct Answer

  6 – 4y

• 2. Mathematically Wrong Number Sentence

  Common Mistake / Misconception

  Find the value of 23 + 4w when w = 3
  23 + 4w
  = 4 × 3 = 12
  = 23 + 12 = 35 (wrong working!)

  Recommended Method

  23 + 4w
  = 23 + 4 × 3
  = 23 + 12
  = 35

• 3. Units Placed Wrongly in Algebraic Answer

  Common Mistake / Misconception

  Susan spent $6y. Amy spent $9. How much did they spend in all?

  $ 6y + 9 or ($6y + $9) or $6y + $9

  Recommended Answer

  $ (6y + 9)

• 4. Plus or Minus?

  Common Mistake / Misconception

  4z – 9 + 3z + 7	= 4z + 3z – 9 + 7
  	= 7z – 16

  Correct Answer

  4z – 9 + 3z + 7	= 4z + 3z – 9 + 7
  	= 7z – 2

• 5. Values with Different Units

  Common Mistake / Misconception

  Tom has a total of $ 1300f. He wants to buy muffins and each muffin costs 25 cents. How many muffins can he buy?

  1300f ÷ 25 = 52f
  (The two values have different units)

  Correct Answer

  25 ÷ 100 = 0.25
  
  1300f ÷ 0.25
  = 5200f
  
  (Ensure both values have the same units before dividing)

• 6. Wrong Assumption of Properties

  Common Mistake / Misconception

  The figure below is made up of two triangles. ∠DAB is twice of ∠CAB and ∠DBA is twice of ∠CBA

  

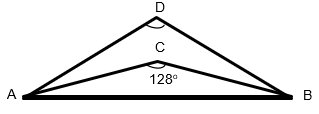
  Pupils see Triangle CAB and Triangle DAB as isosceles triangles.

  Therefore, to them, ∠DAC = ∠CAB = ∠CBA = ∠DBC and they will solve as follows:
  ∠CAB = ∠CBA = (180° – 128°) ÷ 2 = 26°
  ∠DAB + ∠DBA = 26°x 4 = 104°
  ∠ADB = 180° – 104° = 76°

  Note: Though the answer is correct, it will be marked wrong and awarded zero mark as it is a fluke.

  Recommended Method

  Misconception: Do not assume that the 2 triangles are isosceles triangles. This is incorrect as it is not stated explicitly in the question that ADB and ACB are isosceles triangles.

  The correct solution is as follows:

  ∠CAB + ∠CBA
  = 180° – 128° = 52°

  ∠DAB + ∠DBA = 52° × 2 = 104°

  ∠ADB = 180° – 104° = 76°

  Important! Always read the question carefully for any properties or basic shapes stated in the figure given. Do not assume!

• 7. 'Fraction of...' Questions:

  Common Mistake / Misconception

  John has 7 books, Mary has 5 books.

  Express the number of John's books as a fraction of the number of Mary's books.

  Pupils may give the answer as $\frac{5}{7}$ because they believe the numerator has to be smaller than the denominator.

  Misconception: Larger number must be the denominator (wrong!)

  Correct Answer

  Rule: the first number after 'fraction of' is the denominator.

  Answer: $\frac{7}{5}$

• 8. Fraction of Total or Remainder

  Common Mistake / Misconception

  Compare the two questions:

  1. Sarah had $8. She spent $\frac{1}{4}$ of her money on a bag and $\frac{1}{4}$ of it on a purse.
  2. Sarah spent $\frac{1}{4}$ of her money on a bag and $\frac{1}{4}$ of the remainder on a purse.

  Common mistake: Pupils tend to be careless between the 'total' and the 'remainder'.

  Correct Answer

  1. The word "it" refers to $8. (Sarah's total amount of money)
     $\frac{1}{4}$ × $8 = $2
  2. The word "remainder" refers to $\frac{3}{4}$
     $\frac{1}{4}$ × $\frac{3}{4}$ = $\frac{3}{16}$

• 9. Fractions with Units

  Common Mistake / Misconception

  Mrs Tan had $\frac{7}{8}$ kg of flour. She used $\frac{1}{2}$ kg of it to make some cookies. How much flour had she left?

  $\frac{1}{2}$ × $\frac{7}{8}$ = $\frac{7}{16}$ (wrong!)

  Misconception : Pupils always interpret "of it" as a fraction of the total.

  Correct Answer

  $\frac{7}{8}$ – $\frac{1}{2}$ = $\frac{3}{8}$ (correct!)

  Note: Pupils to be alert on the presence or absence of units.

• 10. Remainder Involving Fraction

  Common Mistake / Misconception

  A jug with $\frac{9}{11}$ litres of water is poured into as many glasses of $\frac{3}{8}$ litres each to the brim. How many glasses can be filled to the brim and much water is left in the jug?

  $\frac{9}{11}$ litre ÷ $\frac{3}{8}$ litre

  = $\frac{9}{11}$ × $\frac{8}{3}$ = 2 $\frac{2}{11}$ ≈ 2

  $\frac{2}{11}$ is not the remainder!

  Correct Answer

  $\frac{2}{11}$ × $\frac{3}{8}$ = $\frac{3}{44}$ (This is the remainder)

  Answer: 2 glasses with remaining $\frac{3}{44}$ litre of water is left in the jug.

• 11. Ratio in Wrong Order

  Common Mistake / Misconception

  Sam has $34 and Frank has $35.

  What is the ratio of Frank's money to Sam's money?

  What is the ratio of Frank's money to the total amount of money?

  Tendency to give the ratio answer based on order the numbers appear.

  Recommendation

  Underline the variables in the ratio requested so as to be more careful.

  Example:

  What is the ratio of Frank's money to Sam's money?

  What is the ratio of Frank's money to the total amount of money?

• 12. Answers in the Wrong Format

  Common Mistake / Misconception

  The ratio of the number of boys to the number of girls in the school in 2 : 3. What fraction of the total number of pupils are girls?

  Pupils answer in ratio instead of fraction.

  Recommendation

  Underline what is being requested so as to be more careful.

  Example:

  What fraction of the total number of pupils are girls?

• 13. Using Wrong Original Ratio

  Common Mistake / Misconception

  The ratio of Ali's stamps to John's stamps is 3 : 1. Ali uses 12 stamps and the ratio becomes 3 : 2. How many stamps do they have altogether in the beginning?

  Before	After
  Ali : John	Ali : John
  3 : 1	3 : 2
  6 : 2

  (The variable unchanged is John's stamp)

  3 units = 12

  1 unit = 4

  4 units = 4 × 4 = 16 (solve for wrong number of unit in the old set of ratio)

  Recommendation / Correct Answer

  Before	After
  Ali : John	Ali : John
  3 : 1	3 : 2
  6 : 2

  3 units = 12

  1 unit = 4

  8 units = 8 × 4 = 32

  Should have solved for 8 units instead of 4 units.

  A good practice is to cancel out the original ratio once a new set of equivalent ratio has been derived.