Conquering Fractions in Upper Primary Math - Part 2

This article is a continuation of the previous article whereby I share with you some very common problems faced by students when they learnt concepts on P5 fractions.

If the concepts learnt in P5 Fractions are not strong enough, the lack of understanding in this topic will further compound and affects the learning of more difficult questions on Fractions especially in P6 level.

Do make sure that your child has cleared his/her doubts when learning basic concepts on fractions at P4 and P5 level especially.

In this article, I will be sharing with you the approaches in tackling concepts on ‘fraction of a total’ and ‘fraction of a remainder’ using two simple questions below.

If you read both questions carefully, you will notice that the main difference between the questions lies in the phrase “1/4 of them” for Question 1 and “¼ of the remaining balls” for Question 2.

However, the approach in solving them is entirely different and many P5 students struggle when they first learn these two basic concepts in the topic of P5 fractions!

Let’s analyse them now.

Question 1

1/3 of the balls in a box are red. ¼ of them in the box are yellow and the rest are blue. It there are 30 blue balls, how many balls are there in the box?

Solution

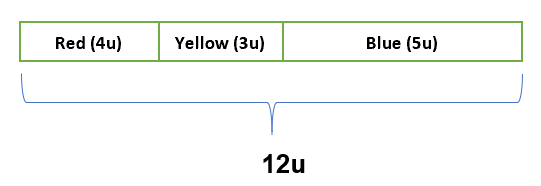
1/3 = 4/12 (4 out of 12 units are red)

1/4 = 3/12 (3 out of 12 units are yellow)

12u – 4u – 3u = 5u

5u = 30

1u = 6

12u = 72 (Answer)

Note

For the following phrases, “1/3 of the balls in a box are red” and “1/4 of them in the box are yellow”, the words “balls” and “them” refer to the total number of balls. Thus, we should find a common denominator for the fractions 1/3 and 1/4.

The denominator of 12 means 12 units represent the total number of balls in the box.

Question 2

1/3 of the balls in a box are red. ¼ of the remaining balls in the box are yellow and the rest are blue. It there are 30 blue balls, how many balls are there in the box?

Solution

3u = 30

1u = 10

6u = 60 (answer)

Note

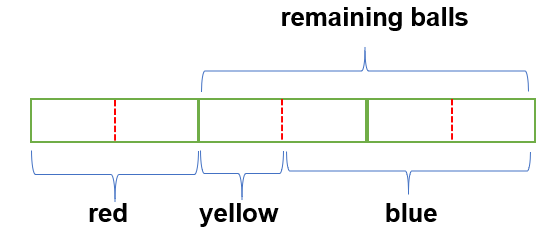
For the following phrases, “1/3 of the balls in a box are red” and “1/4 of the remaining balls in the box…”, we cannot find a common denominator for 3 and 4 as in Question 1.

This is the most common mistake made by many P5 students and they do not understand or know when they should find a common denominator for two fractions in a problem sum.

In this case here, since the words “balls” and remaining balls” clearly do not refer to the same number of balls, we cannot find a common denominator for the two fractions, 1/3 and 1/4.

Note that the 3 original green units need to be split into 6 smaller units indicated by the 3 dotted red lines.

Conclusion

I sincerely hope your child has completely understood the difference in concept between ‘fraction of a total’ and ‘fraction of a remainder’ based on the two simple questions above.

The understanding of these two fundamental concepts will pave the way for solving more complex questions on Fractions in P6 level.