Must-Know Math Question for Primary 4 to PSLE

The following questions were tested in PSLE Math papers around 5 and 10 years ago.

PSLE question around 5 years ago

"Ismail has some cookies. If he gives each of his friends 5 cookies, there is no remainder. If he gives each of them 3 cookies instead, he will have 36 left. How many cookies does Ismail have?"

PSLE question around 10 years ago

"A group of girls shared some sweets among themselves. They tried taking 11 sweets each, but found that the last girl had only 6 sweets. When each girl took 8 sweets, there were 25 sweets left over. How many sweets were there altogether?"

Will this type of question be tested again in PSLE this year? 

Although a question on Excess and Shortage is not frequently tested in PSLE Math paper, questions like the above were frequently tested in school-based Math exam papers and a lot of students found themselves not able to understand and find a way to conquer this particular type of question.

In fact, most students are first exposed to this type of question when they learn Factors and Multiples in P4 Math. However, many of them could not understand and could only use the strategy of Multiples (See Method 2 below) to solve it.

In this article, I am going to share with you 4 different methods on how to conquer a question on Excess and Shortage and I hope you will find a method that suits you most!

To ensure that you get sufficient practice on the mentioned questions, don't miss out OwlSmart's affordable primary school revision subscriptions. You will get instant updates and analysis of your child's revision progress.

Question

Mrs Wong brought some sweets to the class. She distributed the sweets among her pupils in a class. If Mrs Wong gave each of the pupils in the class 6 sweets, she would have 14 sweets left over. If Mrs Wong gave each pupil 8 sweets, she would be short of 10 sweets. How many pupils are there in the class?

1. Understand the problem

Let's break down the problem sum into parts and analyse them...

Mrs Wong brought some sweets to the class. She distributed the sweets among her pupils in a class.

(How many sweets did she have?)

If Mrs Wong gave each of the pupils in the class 6 sweets, she would have 14 sweets left over. – Case 1

If Mrs Wong gave each pupil 8 sweets, she would be short of 10 sweets. – Case 2

(Since the number of sweets in both cases are the same, how do I link them?)

How many pupils are there in the class?

(I am supposed to find the number of pupils in the class)

2. Think of a plan

I am supposed to find out the number of pupils in the class, so let x represent this number.

Since the number of sweets in Case 1 and 2 are the same, I can come up with a mathematical equation using the unknown variable x to link them.

3. Carry it out

Method 1 - Using Algebra

Let the number of pupils in the class be x.
Case 1: Total number of sweets -> 6x + 14
Case 2: Total number of sweets -> 8x – 10

6x + 14 = 8x -10
24 = 2x
X = 12

4. Check my answer

Substitute the value of x into Case 1 and Case 2 respectively to check if the number of sweets is the same.
6x + 14 = 6 ×12 + 14 = 86
8x – 10 = 8 × 12 – 10 = 86

Work backwards
Case 1 ->
86 – 14 = 72
72 ÷ 6 = 12 (My answer is correct!)

More Methods in Solving the Above Question

Method 2 – Using Multiples (You learnt this method in P4!)

Multiples of 6 : 6, 12, 18, 24, ..... 60, 66, 72
Multiples of 6 (+14) : 20, 26, 32, 38, ..... 74, 80, 86

Multiples of 8 : 8, 16, 24, 32, ..... 72, 80, 88, 96
Multiples of 8 (-10) : x, 6, 16, 22, ..... 62, 70, 78, 86

86 – 14 = 72 (total number of sweets)
72 ÷ 6 = 12 (total number of pupils)

Method 3 – Using diagrams

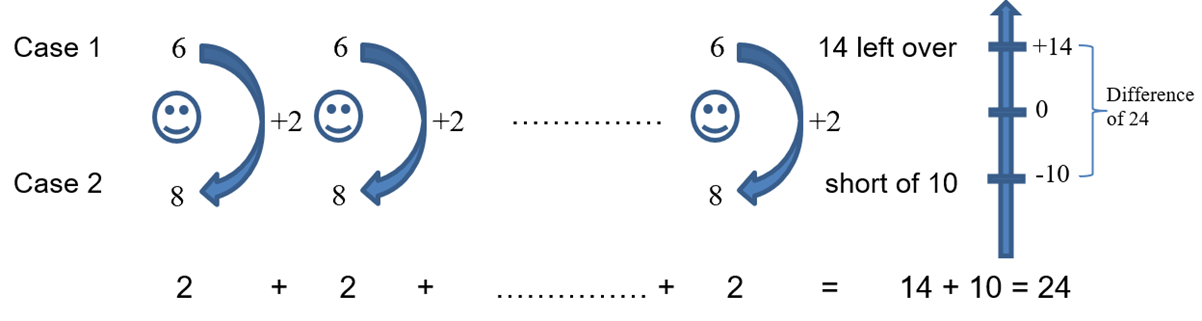
How many groups of 2 will make up the difference of 24? That is the number of pupils in the class.

Solution:
8 – 6 = 2
14 + 10 = 24
24 ÷ 2 = 12

Method 4 – Using Models

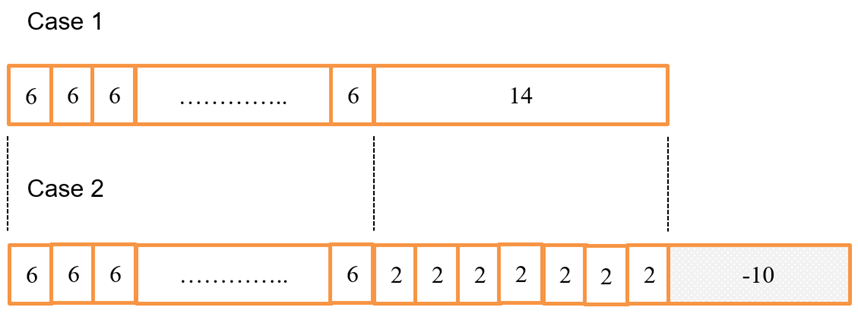
14 ÷ 2 = 7 (groups of 2)
10 ÷ 2 = 5 (groups of 2)
7 + 5 = 12

Conclusion

If you are a P4 or P5 student, you would probably use Method 2 to 4 to solve this particular question type. If you are a P6 student, you would have learnt algebra and I recommend that you use Method 1 to solve it.

Method 2 could be the easiest to understand but it can be very tedious to list out the multiples, especially when the numbers involved are big! For P4 or P5 students, try to use Method 3 though it is the most abstract method to understand.

Again, if you have not already done so, do try out OwlSmart's primary school revision packages which contain the most relevant question types that will almost certainly appear in exams. Many parents and primary school students have benefited from it and I'm sure you will too!